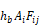
Figure C-1 shows the standard Heat Transfer Engineering
method of determining the long wavelength radiation exchange between black-body
surfaces at uniform temperatures (Oppenheim(1956), Mills(1992)). The areas need
not be equal, or symmetrically disposed, but are drawn that way for simplicity.
The surfaces are assumed to be isothermal, and each surfaces temperature node is
connected to all other surface temperature nodes via conductances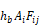
The following methodology is referred to as the “exact” solution in the discussions of Section 2.6. However, it is recognized that it still is an idealization. For instance, surfaces are generally not isothermal. Although the heat transfer qij[Btu/hr], of Equation C-2 is accurate if surfaces i and j are isothermal, the local surface heat transfer qij' [Btu/hr-ft2] on the surfaces is nonuniform because the local view factors are different than the integrated value Fij. For example, if the two surfaces are connected along a common edge, then near the edge qij' will be higher than the average qij/Ai, which will tend to change the temperatures of each wall near the edge faster than away from the edge. For the same reason, the radiation intensities are also non-uniform over a surface, which affects the accuracy of the treatment of the emissivity effects by the Oppenheim surface conductance term, which assumes uniform irradiation.
From the Stefan-Boltzmann equation, the net heat transfer rate between surfaces i and j is:
Equation C- 1
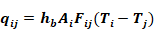
where,
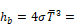
black body radiation coefficient; Btu/(hr-ft2-F).
σ= 0.1714x10^(-8) Btu/hr-ft2-R4, the Stefan-Boltzmann constant.
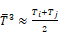
degrees R.
The Fij term is the standard view factor,
equal to the fraction of radiation leaving surface i that is intercepted
by surface j. Fij depends on the size, shape, separation, and orientation
of the surfaces, and at worst requires a double integration. Reciprocity
requires that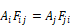
Equation (C-1) is in the linearized form of the
Stefan-Boltzmann equation, where for small temperature differences,
(Ti4-Tj4) is approximated by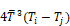
Figure C-1: View-Factor Method’s Radiant Network for Black-Body Surfaces
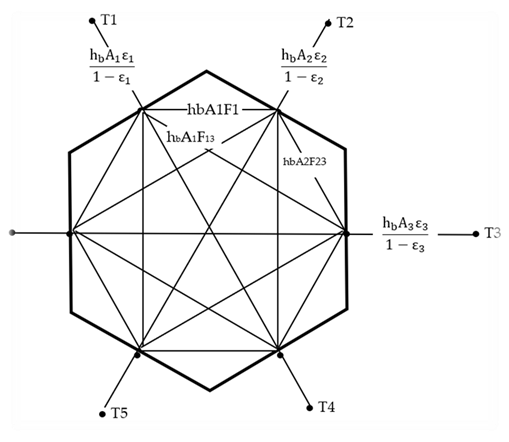
Figure C-2 shows the Figure C-1 black surface case extended
to handle diffuse gray surfaces (ε = α = constant over temperature range of
interest) with emissivities εi, by adding the Oppenheim
radiant surface conductances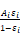
Figure C-2: View-Factor Method’s Network for Grey Surfaces
By dissolving the radiosity nodes using Y-delta
transformations, Figure C-2 converts into Figure C-3 showing the same circuit
form as the black surface circuit of Figure C-1. The transformation
provides the conductances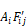
implicit in the conductances of Figure C-2.
Figure C-3: View-Factor Method’s Network for Grey Surfaces Reduced to Star Network
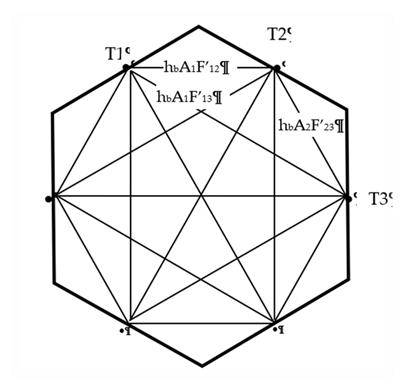
Fij' are the radiant interchange factors. As with the black surfaces view factors, reciprocity holds: AiFij'=Aj Fji'. The net heat transfer between surface i and j (both directly and via reflections from other surfaces) is given by:
Equation C-2
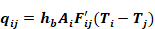
The total net heat transfer from surface i (i.e., the radiosity minus the irradiation for the un-linearized circuit) is given by summing Equation C-2 for all the surfaces seen by surface i, j≠i:
Equation C-3
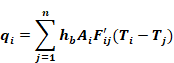
The above methodology is referred to as the “exact” solution
in the discussion of Section 2.6.1.
However, as discussed by Carroll, it is recognized that it is still an
idealization. For instance, surfaces are generally not isothermal.
Although the heat transfer, qij [Btu/hr], of Equation C-2
is accurate if surfaces
 local surface heat transfer qij' q'
[Btu/hr-ft2] on the surfaces is nonuniform because the local view
factors are different than the integrated value Fij For
example, if the two surfaces are connected along a common edge, then near the
edge qij' q will be higher than the average
qij/Ai, which will tend to change the temperatures
of each wall near the edge faster than away from the edge. For the same reason,
the radiation intensities are also non-uniform over a surface, which affects the
accuracy of the treatment of the emissivity effects by the Oppenheim surface
conductance term, which assumes uniform irradiation.
local surface heat transfer qij' q'
[Btu/hr-ft2] on the surfaces is nonuniform because the local view
factors are different than the integrated value Fij For
example, if the two surfaces are connected along a common edge, then near the
edge qij' q will be higher than the average
qij/Ai, which will tend to change the temperatures
of each wall near the edge faster than away from the edge. For the same reason,
the radiation intensities are also non-uniform over a surface, which affects the
accuracy of the treatment of the emissivity effects by the Oppenheim surface
conductance term, which assumes uniform irradiation.